슈테판-볼츠만 법칙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 상세 설명
3. 역사
4. 슈테판-볼츠만 상수
5. 유도
6. 응용 예시
7. 광자 관점에서의 분해
참조

1. 개요

슈테판-볼츠만 법칙은 단위 면적당 방출되는 에너지인 복사 발산도가 절대 온도의 네 제곱에 비례한다는 법칙이다. 이 법칙은 1864년 존 틴들의 실험적 측정을 바탕으로 1877년 요제프 슈테판에 의해 추론되었고, 1884년 루트비히 볼츠만에 의해 이론적으로 유도되었다. 슈테판-볼츠만 상수는 다른 물리 상수로부터 유도되며, 2019년 SI 단위 재정의로 인해 정확한 값을 갖는다. 이 법칙은 태양의 표면 온도 추정, 별의 온도 및 반지름 추정, 지구의 유효 온도 계산 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

멱법칙 - 파레토 분포
파레토 분포는 최솟값 $x_\text{m}$ 과 불평등도 $\alpha$ 로 정의되는 연속 확률분포로, 확률 밀도 함수, 누적 분포 함수 등으로 특징지어지며 지프의 법칙, 파레토 법칙 등과 관련되어 다양한 분야에 응용되고 여러 유형으로 확장될 수 있다.
멱법칙 - 감마 보정
감마 보정은 영상 시스템에서 빛의 강도를 비선형적으로 인코딩 및 디코딩하여 인간 시각의 비선형적 밝기 반응을 보완하고, 디스플레이 장치의 출력 특성을 조정하여 시각적으로 정확한 이미지를 얻는 데 사용되는 기술이다.
온도 방정식 - 열역학 제1법칙
열역학 제1법칙은 닫힌 계의 내부 에너지 변화가 계가 흡수한 열과 계가 한 일의 차이와 같다는 에너지 보존 법칙의 한 측면이다.
온도 방정식 - 열역학 제2법칙
열역학 제2법칙은 외부 도움 없이 저온에서 고온으로 열이 이동하거나 열에너지가 다른 효과 없이 모두 일로 전환되는 순환 과정이 불가능하며, 에너지 흐름의 방향성과 비가역성을 설명하는 클라우지우스 법칙, 켈빈 법칙, 엔트로피 증가 법칙 등으로 표현될 수 있다.
루트비히 볼츠만 - 볼츠만 상수
볼츠만 상수 k는 온도와 에너지를 연결하는 상수이며, 기체 상수와 아보가드로 상수의 비로 정의되고, SI 단위계에서 1.380649×10⁻²³ J/K의 값을 가지며, 거시 물리학과 미시 물리학을 연결하는 중요한 역할을 한다.
루트비히 볼츠만 - 볼츠만 분포
볼츠만 분포는 특정 상태의 확률이 해당 상태의 에너지와 계의 온도의 함수로 주어지는 확률 분포이며, 통계역학, 수학, 경제학 등 다양한 분야에서 활용된다.

슈테판-볼츠만 법칙
일반 정보
이름	슈테판-볼츠만 법칙
분야	열역학, 전자기학
명명자	요제프 슈테판, 루트비히 볼츠만
설명	흑체에서 복사되는 총 에너지와 온도 사이의 관계를 설명하는 물리 법칙
수학적 표현
공식	I = σT⁴
변수	I: 흑체 복사의 표면에서의 복사 강도 (단위 시간당 단위 면적당 방출되는 에너지) σ: 슈테판-볼츠만 상수 (≈ 5.670374419... × 10⁻⁸ W⋅m⁻²⋅K⁻⁴) T: 흑체의 절대 온도 (켈빈 단위)
추가 설명	실제 물체 (흑체가 아닌 물체)의 경우, 방출률 (ε)을 고려해야 하며, 0 ≤ ε ≤ 1. 따라서 I = εσT⁴
관련 개념
관련 항목	흑체 복사 슈테판-볼츠만 상수 빈의 변위 법칙 플랑크의 법칙

2. 상세 설명

복사 발산도(이전에는 ''복사 방출도''라고 불림) ''M''은 단위 시간, 단위 면적당 방출되는 에너지로 정의되며, 에너지 플럭스와 차원이 같다. 국제단위계(SI)에서는 제곱미터당 와트(W/m²)로 표현된다.^[6] 슈테판-볼츠만 법칙에 따르면, 복사 발산도는 절대 온도(T)의 네 제곱에 비례하며, 그 비례 상수를 슈테판-볼츠만 상수(σ)라고 한다.^[6]

물체의 총 방출 전력 ''P''는 복사 발산도에 물체의 표면적 ''A''를 곱하여 계산할 수 있다.^[2]

$P = A \cdot M = A \, \varepsilon\,\sigma\, T^{4}.$

실제 물체는 흑체보다 적은 에너지를 방출하며, 방사율 ''ε''이라는 값을 통해 이를 나타낸다. 방사율은 0과 1 사이의 값을 가지며, 물체의 특성에 따라 달라진다.^[2]

슈테판-볼츠만 법칙은 국소 열역학적 평형(LTE) 상태에 있는 모든 물질에 적용 가능하다.^[2] 키르히호프의 열 복사 법칙에 따라, $\varepsilon \leq 1$ 이 성립한다.^[1]

스펙트럼 방사율이 파장에 관계없이 일정한 물체를 ''회색체''라고 한다.^[2] 실제 물체는 파장에 따라 방사율이 변하는 경우가 많다. 이때 총 방사율은 흑체 방출 스펙트럼을 가중 평균하여 계산할 수 있으며, 이 경우 총 방사율은 온도에 따라 달라질 수 있다.^[2]

파장 및 서브파장 규모 입자,^[3] 메타물질,^[4] 나노구조체^[5] 등은 광선 광학 한계를 벗어나 방사율이 1보다 크게 설계될 수 있다.

복사도는 제곱미터당 스테라디안당 와트(W⋅m⋅sr)로 측정된다. 흑체의 복사도에 대한 슈테판-볼츠만 법칙은 다음과 같다.^[8]^[9]

$L^\circ_\Omega = \frac{M^{\circ}}\pi = \frac\sigma\pi\, T^{4}.$

복사 에너지 밀도에 대한 공식으로 표현된 ''슈테판-볼츠만 법칙''은 다음과 같다.^[10]

$w^\circ_\mathrm{e} = \frac{4}{c} \, M^\circ = \frac{4}{c} \, \sigma\, T^{4} ,$

여기서 $c$ 는 빛의 속도이다.

3. 역사

1864년, 존 틴들은 백금 필라멘트의 적외선 방출량과 필라멘트의 해당 색상에 대한 측정을 발표했다.^[11]^[12]^[13]^[14] 1877년 요제프 슈테판(1835–1893)은 틴들의 실험적 측정을 바탕으로 빈 학술원의 "세션 보고서"에 실린 논문 "Über die Beziehung zwischen der Wärmestrahlung und der Temperatur"("열 복사와 온도의 관계에 관하여")에서 절대 온도의 네제곱에 비례한다는 법칙을 추론했다.^[15]

1884년 루트비히 볼츠만(1844–1906)은 아돌포 바르톨리의 연구를 기반으로 이 법칙을 이론적으로 유도했다.^[16] 바르톨리는 1876년에 열역학의 원리로부터 복사 압력의 존재를 유도했는데, 볼츠만은 이를 바탕으로 이상 기체 대신 전자기 복사를 작동 물질로 사용하는 이상적인 열기관을 고려하여 법칙을 유도하였다.

이 법칙은 발표된 거의 즉시 실험적으로 검증되었다. 하인리히 베버는 1888년에 더 높은 온도에서의 편차를 지적했지만, 1897년까지 1535 K의 온도까지 측정 불확실성 내에서 법칙의 정확성이 확인되었다.^[17] 슈테판-볼츠만 상수를 빛의 속도, 볼츠만 상수 및 플랑크 상수의 함수로 이론적으로 예측하는 이 법칙은 1900년에 공식화된 플랑크 법칙의 직접적인 결과이다.

4. 슈테판-볼츠만 상수

슈테판-볼츠만 상수(σ)는 볼츠만 상수, 플랑크 상수, 진공에서의 빛의 속도와 같은 다른 알려진 물리 상수로부터 유도된다.^[18]^[1]

: $\sigma = \frac{2 \pi^5 k^4}{15 c^2 h^3}$

2019년 SI 단위 재정의로 인해, 슈테판-볼츠만 상수는 정확한 값을 가진다.^[19]

: $\sigma = \left[\frac{2 \pi^5 \left( 1.380\ 649 \times 10^{-23} \right)^4}{15 \left(2.997\ 924\ 58 \times 10^8 \right)^2 \left(6.626\ 070\ 15 \times 10^{-34} \right)^3}\right]\,\frac{\mathrm{W}}{\mathrm{m}^2{\cdot}\mathrm{K}^4}$

따라서, ''σ'' = 5.670374419...×10⁻⁸ W⋅m⁻²⋅K⁻⁴이다.

슈테판-볼츠만 상수의 값은 사용하는 단위계에 따라 다르게 표현된다.^[21]

슈테판-볼츠만 상수, ''σ''
상황	값	단위
SI	5.670374419...×10⁻⁸	W⋅m⁻²⋅K⁻⁴
CGS	5.670374419...×10⁻⁵	erg⋅cm⁻²⋅s⁻¹⋅K⁻⁴
미국 단위계	1.713441...×10⁻⁹	BTU⋅hr⁻¹⋅ft⁻²⋅°R⁻⁴
열화학	1.170937...×10^-7	cal⋅cm⁻²⋅day⁻¹⋅K⁻⁴

5. 유도

5. 1. 열역학적 유도

복사 에너지 밀도가

T^{4}

에 비례한다는 슈테판-볼츠만 법칙은 열역학을 사용하여 유도할 수 있다.^[31]^[14] 이 유도는 복사 압력 ''p''와 내부 에너지 밀도

u

사이의 관계인

p = \frac{u}{3}

를 이용한다. 이 관계는 전자기 응력-에너지 텐서의 형태를 사용하여 보일 수 있다.

열역학적 기본 관계

dU = T \, dS - p \, dV

에서

dV

로 나누고

T

를 고정하면,

\left(\frac{\partial U}{\partial V}\right)_T = T \left(\frac{\partial S}{\partial V}\right)_T - p = T \left(\frac{\partial p}{\partial T}\right)_V - p

를 얻는다. 여기서 마지막 등식은 맥스웰 관계

\left(\frac{\partial S}{\partial V}\right)_T = \left(\frac{\partial p}{\partial T}\right)_V

에서 유도된다.

에너지 밀도의 정의

U = u V

에서, 복사의 에너지 밀도는 온도에만 의존하므로

\left(\frac{\partial U}{\partial V}\right)_T = u \left(\frac{\partial V}{\partial V}\right)_T = u

이다. 따라서,

u = T \left(\frac{\partial p}{\partial T}\right)_V - p

가 성립한다.

p = \frac{u}{3}

를 위 식에 대입하고 정리하면, 부분 미분

\left(\frac{\partial u}{\partial T}\right)_V

는

u

와

T

사이의 관계, 즉

\frac{du}{4u} = \frac{dT}{T}

로 표현될수 있고, 이를 풀면

u = A T^4

가 얻어진다. (

A

는 적분 상수)

총 에너지 밀도 ''U''는

U = \frac{4}{c} \, \sigma \, T^4

로 주어지며, 여기서 곱

\frac{4}{c} \sigma

는 복사 상수 또는 복사 밀도 상수라고도 불린다.

이 법칙은 광자 기체의 에너지 밀도 와 압력 의 관계인

p=\frac{u}{3}

로부터 유도할 수 있다. 이것과 를 열역학적 상태 방정식

\left( \frac{\partial U}{\partial V} \right)_T =T\left( \frac{\partial p}{\partial T} \right)_V -p

에 대입하여 미분 방정식

\frac{du}{dT} =\frac{4u}{T}

을 얻을 수 있다. 이것을 풀면

u\propto T^4

이 유도된다.

5. 2. 플랑크 법칙으로부터의 유도

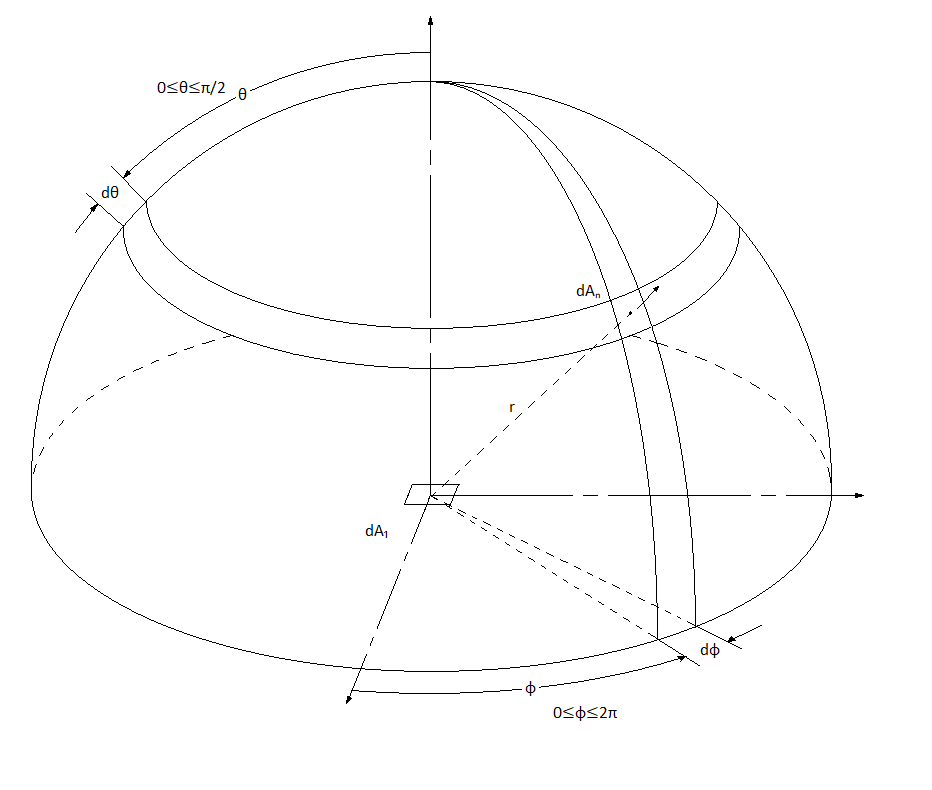
슈테판-볼츠만 법칙은 작은 평평한 흑체 표면이 반구로 복사하는 것을 고려하여 유도할 수 있다. 이 유도에서는 구면 좌표계를 사용하며, ''θ''는 천정각이고 ''φ''는 방위각이다. 작은 평평한 흑체 표면은 xy 평면에 놓여 있으며, 여기서 ''θ'' = ^π/₂이다.

흑체 표면에서 방출되는 빛의 세기는 플랑크 법칙에 의해 주어진다.

:

I(\nu,T) =\frac{2 h\nu^3}{c^2}\frac{1}{ e^{h\nu/(kT)}-1}

여기서,

$I(\nu,T)$ 는 흑체가 온도 ''T''에서 주파수 $\nu$ 로 방출하는 단위 표면적, 단위 입체각, 단위 주파수당 에너지이다.
$h$ 는 플랑크 상수이다.
$c$ 는 광속이며,
$k$ 는 볼츠만 상수이다.

량

I(\nu,T) ~A \cos \theta ~d\nu ~d\Omega

는 면적 A의 표면이 입체각 ''d''Ω을 통해 ν와 ''ν'' + ''dν'' 사이의 주파수 범위에서 복사하는 에너지이다.

슈테판-볼츠만 법칙은 방출체의 단위 면적당 방출되는 에너지를 제공한다.

:

\frac{P}{A} = \int_0^\infty I(\nu,T) \, d\nu \int \cos \theta \, d\Omega

흑체는 람베르트 (즉, 람베르트 코사인 법칙을 따른다)이므로 코사인이 나타난다. 즉, 구를 따라 관찰된 세기는 실제 세기에 천정각의 코사인을 곱한 값이다.

슈테판-볼츠만 법칙을 유도하기 위해 우리는

d\Omega = \sin \theta\, d\theta \, d\varphi

를 반구에 대해 적분하고

\nu

를 0에서 ∞까지 적분해야 한다.

:

\begin{align}\frac{P}{A} & = \int_0^\infty I(\nu,T) \, d\nu \int_0^{2\pi} \, d\varphi \int_0^{\pi/2} \cos \theta \sin \theta \, d\theta  \\& = \pi \int_0^\infty I(\nu,T) \, d\nu\end{align}

''I''에 대입하면,

:

\frac{P}{A} = \frac{2 \pi h}{c^2} \int_0^\infty \frac{\nu^3}{ e^{\frac{h\nu}{kT}} - 1} \, d\nu

를 얻는다.

이 적분을 평가하기 위해 치환한다.

:

\begin{align}u & = \frac{h \nu}{k T} \\[6pt]du & = \frac{h}{k T} \, d\nu\end{align}

그러면 다음이 얻어진다.

:

\frac{P}{A} = \frac{2 \pi h }{c^2} \left(\frac{k T}{h} \right)^4 \int_0^\infty \frac{u^3}{ e^u - 1} \, du .

오른쪽의 적분은 표준이며, 보즈-아인슈타인 적분, 폴리로그 또는 리만 제타 함수

\zeta(s)

의 특수한 경우이다. 적분의 값은

\Gamma(4)\zeta(4) = \frac{\pi^4}{15}

(여기서

\Gamma(s)

는 감마 함수이다)이며, 완전한 흑체 표면에 대해 다음을 얻는다.

:

M^\circ= \sigma T^4 ~, ~~\sigma = \frac{2 \pi^5 k^4 }{15 c^2 h^3}= \frac{\pi^2 k^4}{60 \hbar^3 c^2}.

이 증명은 작은 평평한 표면만 고려하여 시작되었지만, 모든 미분 가능 다양체는 작은 평평한 표면들의 집합으로 근사할 수 있다. 표면의 기하학이 흑체가 자신의 복사를 재흡수하게 하지 않는 한, 방출되는 총 에너지는 각 표면에서 방출되는 에너지의 합과 같고, 총 표면적은 각 표면의 면적의 합과 같다. 따라서 이 법칙은 표면이 전체적으로 동일한 온도를 갖는 한 모든 볼록 집합 흑체에도 적용된다. 이 법칙은 볼록 껍질이 흑체인 것처럼 복사한다는 사실을 사용하여 비볼록 물체에서 방출되는 복사로 확장된다.

총 에너지 밀도 ''U''는, 적분 범위가 전체 구면이고 코사인이 없으며, 에너지 플럭스(U c)를 속도 ''c''로 나누어 에너지 밀도 ''U''를 구해야 한다.

:

U = \frac{1}{c} \int_0^\infty I(\nu,T) \, d\nu \int \, d\Omega

따라서

\int_0^{\pi/2} \cos \theta \sin \theta \, d\theta

는

\int_0^{\pi} \sin \theta \, d\theta

로 대체되어 추가 인자 4가 생성된다.

총합은 다음과 같다.

:

U = \frac{4}{c} \, \sigma \, T^4

곱

\frac{4}{c} \sigma

는 '''복사 상수''' 또는 '''복사 밀도 상수'''라고도 한다.

플랑크 법칙에 따르면, 진동수 ν로 나타낸 복사 발산도의 스펙트럼은

:

I(\nu,T) = \frac{2h}{c^2}\frac{\nu^3}{\mathrm{e}^{h\nu/kT} -1}

로 주어지며,

제타 함수의 특수 값에 대한 지식을 사용하여 적분을 계산하면,

:

\int_0^\infty \frac{x^3}{\mathrm{e}^x -1} dx = \Gamma(4) \zeta(4)=6 \cdot \frac{\pi^4}{90} =\frac{\pi^4}{15}

가 된다.

따라서, 슈테판-볼츠만 상수는

:

\sigma =\frac{2\pi^5k^4}{15c^2h^3}

로 계산된다.

5. 3. 빈 근사 및 레일리-진스 근사에 의한 계산

빈 공식은 고주파수 영역에서의 근사식으로,

f(x) =\mathrm{e}^{-x}

형태를 가지며, 적분은

\int_0^\infty x^3\,\mathrm{e}^{-x} dx =\Gamma(4) =6

이 된다. 두 복사 상수가 플랑크 법칙에 기초한 값과 같다고 가정하여 슈테판-볼츠만 상수를 계산하면

\sigma_\text{Wien} =\frac{12\pi k^4}{c^2h^3}=\frac{\sigma}{\zeta(4)} =\frac{\sigma}{1.0823\ldots}

이 되며, 플랑크의 법칙으로부터 유도한 값과 비교하여 약간 작은 값이 된다.

레일리의 공식은 저주파수 영역에서의 근사식이며,

f(x) =\frac{1}{x}

의 형태를 띤다. 적분은

\int_0^\infty x^2 dx

이며, 발산한다.

6. 응용 예시

6. 1. 태양의 표면 온도 추정

슈테판-볼츠만 법칙을 이용하면 태양의 표면 온도를 추정할 수 있다. 슈테판은 이 법칙을 사용하여 태양 표면 온도를 약 5700 K로 추정했다.^[22] 그는 자크 루이 소레의 데이터를 통해 태양으로부터의 에너지 플럭스 밀도가 특정 가열된 금속 라멜라의 에너지 플럭스 밀도보다 29배 더 크다는 것을 알아냈다.^[23] 소레는 라멜라의 온도를 약 1900 °C에서 2000 °C로 추정했다. 슈테판은 태양으로부터의 에너지 플럭스의 1/3이 지구 대기에 흡수된다고 보정하여, 소레의 값보다 3/2배 더 큰 43.5를 태양의 에너지 플럭스로 간주했다.

최대 방출 파장과 복사 발산도의 대수-대수 그래프 대 흑체 온도. 빨간색 화살표는 광구의 5780 K 흑체가 501 nm 피크와 63.3 MW/m² 복사 발산도를 갖는다는 것을 보여준다.

2. 57⁴ = 43.5이므로, 이 법칙에 따르면 태양의 온도는 라멜라의 온도보다 2.57배 더 높다. 따라서 슈테판은 5430 °C (5700 K)라는 값을 얻었다. 이는 태양 온도에 대한 최초의 합리적인 값이었다.^[24] 1838년 클로드 푸이예는 뒬롱-프티 법칙을 사용하여 1800 °C라는 낮은 값을 결정하기도 했다.^[25]^[26]

태양 상수, 태양과 지구 사이의 거리, 태양의 반지름 등을 이용하면, 다음과 같이 표면 온도를 계산할 수 있다.

태양이 시간당 방출하는 전자기파의 복사 에너지(광도) ''L''_s는, 태양의 반지름을 ''R''_s라고 하면 태양의 표면적은 4π''R''_s²이므로, 태양을 흑체로 가정하고 슈테판-볼츠만 법칙에 따라 태양의 표면 온도를 ''T''로 하여

:''L''_s = 4π''R''_s² × σ''T''⁴

로 나타낼 수 있다.

지구 부근에서 태양 방향을 향한 면에 대한 복사 조도 ''E''는 태양 상수라고 불리는 양이며, 대기권 밖의 인공위성에 의한 관측으로 그 값이 알려져 있다.

태양과 지구의 거리를 ''a''라고 하면, 복사 조도의 복사 강도 ''I''로의 환산은

:''I'' = ''a''²''E''

가 된다. 복사 강도를 모든 방향에 대해 합하면 전체 복사속이 된다. 태양이 모든 방향으로 동일하게 방출한다고 생각하면, 전체 입체각 4π를 곱하여

:''L''_s = 4π''I'' = 4π''a''²''E''

가 된다.

따라서 태양의 표면 온도는

:''T'' = ⁴√(''E''/σ × ''a''²/''R''_s²)

로 나타낼 수 있다.

각각의 상수 값^[37], 태양 상수 ''E''=1.37×10³ W/m², 궤도 긴반지름 ''a''=1.496×10¹¹ m, 태양 반지름 ''R''_s=6.960×10⁸ m를 대입하면, 표면 온도는

:''T'' ≃ 5780 K

로 계산된다.

6. 2. 별의 온도 및 반지름 추정

슈테판-볼츠만 법칙은 별의 온도와 반지름을 추정하는 데에도 활용된다.^[27] 별을 흑체로 가정하면, 별의 광도(광도) ''L'', 유효 온도(유효 온도) ''T'', 반지름 ''R'' 사이에는 다음과 같은 관계가 성립한다.

:

L = 4 \pi R^2 \sigma T^4

여기서 ''σ''는 슈테판-볼츠만 상수이다. 이 식을 변형하여 별의 온도를 계산할 수 있다.

:

T = \sqrt[4]{\frac{L}{4 \pi R^2 \sigma}}

또는 별의 반지름을 계산할 수 있다.

:

R = \sqrt{\frac{L}{4 \pi \sigma T^4}}

태양에 대한 매개변수를 이용하여 식을 단순화하면 다음과 같다.

:

\begin{align}\frac{L}{L_\odot} &= \left(\frac{R}{R_\odot}\right)^2 \left(\frac{T}{T_\odot}\right)^4 \\[1ex]\frac{T}{T_\odot} &= \left(\frac{L}{L_\odot}\right)^{1/4} \left(\frac{R_\odot}{R}\right)^{1/2} \\[1ex]\frac{R}{R_\odot} &= \left(\frac{T_\odot}{T}\right)^2 \left(\frac{L}{L_\odot}\right)^{1/2}\end{align}

여기서

R_\odot

는 태양 반지름이다.

표면적 ''A''와 복사 발산도

M^{\circ}

를 사용하여 식을 다시 작성할 수도 있다.

:

\begin{align}L &= A M^{\circ} \\[1ex]M^{\circ} &= \frac{L}{A} \\[1ex]A &= \frac{L}{M^{\circ}}\end{align}

여기서

A = 4 \pi R^2

이고

M^{\circ} = \sigma T^{4}.

이다.

이러한 관계식을 통해 천문학자들은 별의 반지름을 추론할 수 있다. 슈테판-볼츠만 법칙은 블랙홀 열역학에서 호킹 복사를 설명하는 데에도 사용된다.

6. 3. 지구의 유효 온도 계산

흑체 근사를 통해 지구의 유효 온도를 계산할 수 있다. 태양의 광도(

L_\odot

)는

L_\odot = 4\pi R_\odot^2 \sigma T_\odot^4

이며, 지구에서 이 에너지는 지구와 태양 사이의 거리(

a_0

)를 반지름으로 하는 구를 통과한다. 이때 복사 조도(단위 면적당 수신된 전력)는

E_\oplus = \frac{L_\odot}{4\pi a_0^2}

이다. 지구의 반지름(

R_\oplus

)을 고려하면, 지구에 흡수되는 복사속은

\Phi_\text{abs} = \pi R_\oplus^2 \times E_\oplus

이다.

슈테판-볼츠만 법칙에 따라 지구에서 방출되는 플럭스와 흡수되는 플럭스가 같아지는 정상 상태를 가정하면,

4\pi R_\oplus^2 \sigma T_\oplus^4 = \pi R_\oplus^2 \times \frac{4\pi R_\odot^2\sigma T_\odot^4}{4\pi a_0^2}

이고,

이를 통해 지구의 유효 온도(

T_\oplus

)를 다음과 같이 구할 수 있다.

T_\oplus = T_\odot \times \sqrt\frac{R_\odot}{2 a_0} \approx 279 \; {\rm K}

이는 지구 표면의 유효 온도가 6 °C임을 나타내며, 모든 방출을 완벽하게 흡수하고 대기가 없다고 가정한 결과이다.

지구는 0.3의 알베도를 가지고 있어, 지구에 도달하는 태양 복사의 30%가 흡수되지 않고 우주로 산란된다.^[28]^[29] 알베도를 고려하면 유효 온도는 약 255K로 감소한다.^[28]^[29] 온실 효과로 인해 지구의 실제 평균 표면 온도는 약 288K로, 255K의 유효 온도보다 높다.^[30]

지표면에 있는 흑체 표면이 햇빛과 평형을 이루는 경우, 태양이 천정에 있고 표면이 수평일 때 복사 조도는 최대 1120 W/m²까지 올라갈 수 있으며,^[30] 이때 슈테판-볼츠만 법칙으로 계산한 온도는 약 375K (102 °C)이다.^[30]

7. 광자 관점에서의 분해

슈테판-볼츠만 법칙은 다음과 같이 표현될 수 있다.^[34]

: $M^{\circ} = \sigma\, T^4 = N_\mathrm{phot} \, \langle E_\mathrm{phot} \rangle$

여기서 광자의 플럭스, $N_\mathrm{phot}$ 는 다음과 같다.

: $N_\mathrm{phot} = \pi \int_0^\infty \frac{B_\nu}{h\nu}\,\mathrm{d}\nu$

: $N_\mathrm{phot} = \left({ 1.5205\times10^{15}} \; \textrm{photons}{\cdot}\textrm{s}^{-1}{\cdot}\textrm{m}^{-2}{\cdot}\mathrm{K}^{-3}\right)\cdot T^3$

그리고 광자당 평균 에너지, $\langle E_\textrm{phot}\rangle$ 는 다음과 같다.

: $\langle E_\textrm{phot}\rangle = \frac{\pi^4}{30\,\zeta(3)} k\,T= \left({3.7294 \times 10^{-23}} \mathrm{J}{\cdot}\mathrm{K}^{-1}\right) \cdot T\,.$

Marr과 Wilkin(2012)은 학생들이 빈의 변위 법칙을 배우는 대신 $\langle E_\textrm{phot}\rangle$ 에 대해 배우고, 슈테판-볼츠만 법칙을 배울 때 위 분해를 가르치도록 권장한다.^[34]

참조

_[1] 서적 Fundamentals of Statistical and Thermal Physics Waveland Press 1965
_[2] 서적 Thermal Radiation Heat Transfer Taylor & Francis 1992
_[3] 서적 Absorption and scattering of light by small particles https://books.google[...] Wiley
_[4] 간행물 Conference on Lasers and Electro-Optics 2012 Optical Society of America
_[5] 논문 Heat radiation from long cylindrical objects https://link.aps.org[...] 2012
_[6] 웹사이트 Thermal insulation — Heat transfer by radiation — Vocabulary https://www.iso.org/[...] International Organization for Standardization 2023-06-17
_[7] 웹사이트 radiant exitance https://www.electrop[...] International Electrotechnical Commission 2023-06-20
_[8] 서적 Atmospheric Radiation: Theoretical Basis Oxford University Press 1989
_[9] 웹사이트 A Primer on Atmospheric Radiative Transfer: Chapter 3. Radiometric Basics http://eodg.atm.ox.a[...] Earth Observation Data Group, Department of Physics, University of Oxford 2023-06-15
_[10] 웹사이트 Radiation Energy Density http://hyperphysics.[...] 2023-06-20
_[11] 논문 On luminous [i.e., visible] and obscure [i.e., infrared] radiation https://babel.hathit[...] 1864
_[12] 서적 Lehrbuch der Experimentalphysik https://babel.hathit[...] B.G. Teubner 1875
_[13] 인용
_[14] 논문 Heat radiation law – from Newton to Stefan http://nopr.niscair.[...] 2023-06-15
_[15] 인용
_[16] 논문 Ableitung des Stefan'schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie https://babel.hathit[...] 1884
_[17] 서적 The Bumpy Road: Max Planck from Radiation Theory to the Quantum (1896–1906) https://books.google[...] Springer International Publishing 2023-06-15
_[18] 웹사이트 Thermodynamic derivation of the Stefan–Boltzmann Law https://www.tec-scie[...] 2023-06-20
_[19] 웹사이트 A081820 https://oeis.org/A08[...]
_[20] 논문 Measurement of the Universal Gas Constant ''R'' Using a Spherical Acoustic Resonator http://researchrepos[...] 1988-01-25
_[21] 서적 Heat and Mass Transfer: a Practical Approach McGraw Hill
_[22] 인용
_[23] 서적 Comparaison des intensités calorifiques du rayonnement solaire et du rayonnement d'un corps chauffé à la lampe oxyhydrique https://babel.hathit[...] Archives des sciences physiques et naturelles 1872
_[24] 논문 An account of observations on solar radiation https://books.google[...] 1862
_[25] 논문 Mémoire sur la chaleur solaire, sur les pouvoirs rayonnants et absorbants de l'air atmosphérique, et sur la température de l'espace https://www.biodiver[...] 1838
_[26] 서적 Scientific Memoirs, Selected from the Transactions of Foreign Academies of Science and Learned Societies, and from Foreign Journals https://books.google[...] Johnson Reprint Corporation 2023-06-15
_[27] 웹사이트 Luminosity of Stars http://outreach.atnf[...] Australian Telescope Outreach and Education 2006-08-13
_[28] 보고서 Intergovernmental Panel on Climate Change Fourth Assessment Report. Chapter 1: Historical overview of climate change science http://www.ipcc.ch/p[...]
_[29] 웹사이트 Solar Radiation and the Earth's Energy Balance http://eesc.columbia[...] 2010-08-16
_[30] 웹사이트 Introduction to Solar Radiation http://www.newport.c[...] Newport Corporation
_[31] 웹사이트 Derivation of the Stefan–Boltzmann Law http://www.pha.jhu.e[...] 2018-09-03
_[32] 서적 On the Trail of Blackbody Radiation: Max Planck and the Physics of his Era https://books.google[...] MIT Press 2022-09-13
_[33] 논문 The association of GRB 060218 with a supernova and the evolution of the shock wave 2006-08
_[34] 논문 A Better Presentation of Planck's Radiation Law https://scholarship.[...] 2012
_[35] 웹사이트 CODATA Value https://physics.nist[...]
_[36] 서적 『物理学辞典』
_[37] 간행물 『理科年表』

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com